Adjoint representation of a Lie group
Every Lie group have a canonical group representation.
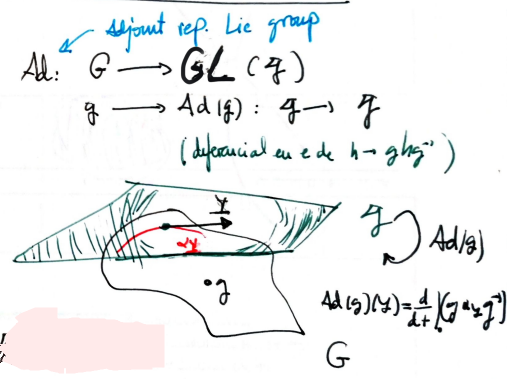
Given a Lie group $G$, every $g\in G$ determines a smooth group homomorphism of $G$ onto itself, $C_g \in \mbox{Aut}(G)$, by means of the assignation
$$ L_g \circ R_{g^{-1}}:h \mapsto ghg^{-1} $$If we consider the differential of this map at the identity we can define:
$$ Ad_g:=d(L_g \circ R_{g^{-1}})_e:T_e G \cong \mathfrak{g} \longrightarrow T_e G \cong \mathfrak{g} $$And so we have defined an morphism $G \longmapsto GL(\mathfrak{g})$, and we have a group representation of $G$.
Explicitly, and taking into account the exponential map, we have
$$ \begin{array}{rcl} Ad_g:\mathfrak{g}& \longrightarrow & \mathfrak{g}\\ V & \longrightarrow & \frac{d}{dt}(g e^{tV}g^{-1})|_{t=0}\\ \end{array} $$Idea
Given $V \in \mathfrak{g}$, we can think of it like a curve $\alpha(t)$ emanating from $e\in G$ with velocity $V$. Then, for $g\in G$ we have another curve $\beta(t)=g\alpha(t) g^{-1}$. The assignation
$$ V\mapsto \beta'(0) $$is a linear map from $\mathfrak{g}$ to $\mathfrak{g}$, that is, a representation.
To _see the action_ of $g$ over $V$ think of the action of $g$ over any space $M$ it acts (you can choose the proper $G$). In a point $P \in M$ you can act with $V$ to begin a little curve that arrive to a very near point $Q$. But you can, instead, begin at $P$, go back to $g^{-1} P$, start the little curve produced with $h$ and apply $g$ to the final point. You will have obtained a another point different from $Q$, say $Q'$. The little curve starting at $P$ toward $Q'$ is that produced by $gVg^{-1}$.
Ad(G)-module structure
Since $Ad(G)=\{Ad_g: g\in G\}$ is a subring of $End(\mathfrak{g})$ then $\mathfrak{g}$ has the structure of a $Ad(G)$-module.
If $H$ is a subgroup of $G$ then it has also the structure of a $Ad(H)$-module.
Adjoint representation of a Lie algebra
Given the adjoint representation of the Lie group $G$ as above, we have
$$ Ad: G \rightarrow GL(\mathfrak{g}) $$which is a Lie group homomorphism. So we can think of the differential at identity
$$ d(Ad)_e:T_e G \rightarrow T_{id} GL(\mathfrak{g}), $$expression that, after defining $ad:=d(Ad)_e,$ can be rewritten as
$$ ad: \mathfrak{g} \rightarrow \mathfrak{gl(g)} $$Explicitly, given $X,Y \in \mathfrak{g}$, and by using the exponential map
$$ ad(X)(Y)=\frac{d}{ds}|_{s=0} \left(Ad_{e^{sX}}(Y)\right)=\frac{d}{ds}|_{s=0} \left(Ad_{e^{sX}}(\frac{d}{dt}|_{t=0}e^{tY})\right)= $$ $$ =\frac{d}{ds} \frac{d}{dt}|_{s,t=0} \left(e^{sX}e^{tY}e^{-sX}\right) $$This expression can be simplified even further. Since $ad(X)(Y) \in T_e G$ consider a smooth function $f$ defined in an open neighbourhood of $e\in G$. Then
$$ ad(X)(Y)(f)=\frac{d}{ds} \frac{d}{dt}|_{s,t=0} \left(f(e^{sX}e^{tY}e^{-sX})\right) \tag{1} $$Now, observe that if $F(t_1,t_2)$ is a function of two real variables, by the chain rule
$$ \frac{d}{ds}|_{s=0}F(s,-s)=\partial_{t_1}F(t_1,0)|_{t_1=0}-\partial_{t_2}F(0,t_2)|_{t_2=0} $$So now, if we fix $t$ in $(1)$ and apply the chain rule to $s$ we obtain
$$ \frac{d}{dt}|_{t=0}\left(\frac{d}{ds}|_{s=0} f(e^{sX}e^{tY})-\frac{d}{ds}|_{s=0} f(e^{tY}e^{sX})\right) $$Remember that for a smooth function $g$ and $\hat{X}$ a left invariant vector field extending $X\in \mathfrak{g}$
$$ \frac{d}{ds}|_{s=0}(g(h e^{sX}))=\hat{X}(g)(h) $$(see exponential map). Therefore
$$ \frac{d}{dt}|_{t=0}\frac{d}{ds}|_{s=0} f(e^{sX}e^{tY})=\frac{d}{ds}|_{s=0}(\hat{Y}(f)(e^{sX}))= $$ $$ =\hat{X}(\hat{Y}(f)(e)) $$and
$$ \frac{d}{dt}|_{t=0}\frac{d}{ds}|_{s=0} f(e^{tY}e^{sX})=\frac{d}{dt}|_{t=0}(\hat{X}(f)(e^{tY}))= $$ $$ =\hat{Y}(\hat{X}(f)(e)) $$and so
$$ ad(X)(Y)(f)=[X,Y](f). $$(Reference: Bump, Lie Groups, proposition 8.2, page 49.)
Finally, I think that the adjoint representation of a Lie algebra is a particular case of Lie algebra action.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: